Le cycliste averti sait qu’on a intérêt à augmenter la puissance dans les montées et à se relâcher dans les descentes pour optimiser sa vitesse moyenne, mais ceci reste-t-il vrai lorsque l’on affronte un vent de face?
Quand on affronte un fort vent de face, vaut-il mieux faire le gros dos, continuer à exercer la même puissance, et attendre que ça passe, ou au contraire, appuyer plus fort, quitte à se relâcher un peu lorsque l’on aura le vent dans le dos?
La réponse est: oui, il faut appuyer plus fort, mais pas tant que ça… Démonstration.
D’abord, il convient de reformuler scientifiquement le problème.
Dans le cas général, la puissance à fournir en vélo peut se décomposer en 3 termes:
P = P_Air + P_Mécanique + P_Pente
avec
P_Air = puissance utilisée pour vaincre la résistance de l’air
P_Mécanique = puissance nécessaire pour vaincre les frottements mécaniques (organes de transmission du vélo et frottements des pneus sur la route)
P_Pente = puissance nécessaire pour gravir la pente
On a:
P_Air = 1/2 . ro . S . Cx . V . (V-Vent)^2
avec
ro = masse spécifique de l’air = 1,205 kg/m^3 (à 21°C et 1 bar de pression)
S = surface frontale (de l’ensemble cycliste + vélo)
Cx = coeff aérodynamique (de l’ensemble cycliste + vélo)
V = vitesse du cycliste (en m/s)
Vent = vitesse du vent (en m/s, positive si dans le sens du cycliste, négative sinon)
Le coeff S.CX dépend du profil du vélo, plus ou moins aérodynamique, mais surtout de la position de cycliste. Un cycliste amateur peut avoir un S.Cx de 0,43 m², un pro de 0,36 m².
Nous avons retenu à titre d’exemple un S.Cx de 0,38m².
P_Frottements = m.g.V.K
avec
m = masse du cycliste + vélo
g = constante gravitationnelle
K = paramètre dépendant du vélo et du revêtement de la route
C’est ici que s’exprime la différence entre les vélos. Pour un vélo bas de gamme, K est de l’ordre de 0,01. Pour un vélo haut de gamme, K est inférieur à 0,008. C’est cette valeur que nous avons retenu dans notre modélisation.
Si l’on veut aller dans les détails, la puissance due au frottement peut être décomposée en différentes composantes, dont la principale est la résistance au roulement. Cette dernière dépend essentiellement de la nature du revêtement et du pneu (ou boyau utilisé).
La résistance au roulement est égale à:
Crr.m.g.V
avec Crr = Coefficient de résistance au roulement. Crr varie entre 0,0038 et 0,0080.
P_Pente = m.g.V.p
avec
p = pente (en %)
Soit au total:
P = 1/2 . ro . S . Cx . V . (V-Vent)^2 + m.g.V.K + m.g.V.p
Dans ce qui suit, on va considérer un trajet aller-retour. L’aller se fera avec un vent de vitesse Vent, et le retour se fera avec un vent de vitesse -Vent.
A l’aller:
vitesse cycliste = V1
vitesse vent = Vent
puissance développée = P1
distance parcourue = d
Au retour:
vitesse cycliste = V2
vitesse vent = -Vent
puissance développée = P2
distance parcourue = d
Ce que l’on cherche à optimiser, c’est la vitesse moyenne sur le parcours, soit:
V = 2.V1.V2/(V1+V2) – voir http://silberblog.graphz.fr/horreur-mathematique-durete-du-velo
La contrainte que l’on a, c’est de le faire à « coût physiologique » constant.
Là, il y a là une petite subtilité.
On pourrait se dire que l’on va essayer d’optimiser sa course à coût énergétique constant. Dans ce cas, sa reviendrait à dire que l’on essaierait de garder une puissance moyenne constante, et que l’on essaierait ensuite de déterminer l’allocation optimale de puissance entre l’aller et le retour pour maximiser la vitesse moyenne.
Mais les choses ne sont pas si simples. Il est plus éprouvant pour l’organisme de faire 10′ @150W + 10’@250W, ou de faire 10x(1’@300W + 1’@100W), que de faire 20’@200W, même si tous ces exercices ont une durée et une puissance moyenne équivalentes.
Ceci a été traduit par Andrew Coggan par la notion de Normalized Power (NP), qui représente à peu près le coût physiologique d’une séance où la puissance varie. Sur la notion de NP, voir http://home.trainingpeaks.com/articles/cycling/normalized-power,-intensity-factor,-training-stress-score.aspx
Si vous faîtes une séance d’1H à 200W de NP, ça revient à peu près à avoir roulé pendant 1h à puissance constante de 200W – même si en réalité votre puissance a beaucoup varié au cours de la séance, et si votre puissance moyenne a été bien inférieure à 200W. Typiquement, sur une course vélo, avec de nombreuses accélérations et démarrages, on aura une puissance moyenne faible, mais une NP élevée, qui traduira bien mieux la sollicitation réelle de l’organisme que la puissance moyenne.
L’algorithme du calcul de la NP est donné par Andrew Coggan lui-même ici:
http://forum.slowtwitch.com/cgi-bin/gforum.cgi?post=3097774br
C’est assez compliqué (il faut lisser le calcul de la puissance en calculant une moyenne mobile sur 30s, puis faire la racine 4ème de la moyenne des puissances 4ème des moyennes ainsi obtenues…) mais ça se simplifie pas mal lorsque l’on suppose que l’on n’a que 2 sections sur lesquelles on roule à puissance constante.
Si on roule une durée t1 à puissance P1 et vitesse V1 et une durée t2 à P2 et V2, on a:
NP = ((t1.P1^4 + t2.P2^4)/(t1+t2))^(1/4)
soit vu que d=V1.t1 = V2.t2:
NP = ((V2.P1^4 + V1.P2^4)/(V1+V2))^(1/4)
Au total, le problème peut donc être ainsi reformulé:
« Quelle est l’allocation optimale de puissance entre l’aller et le retour qui maximise la vitesse moyenne tout en maintenant une NP constante? »
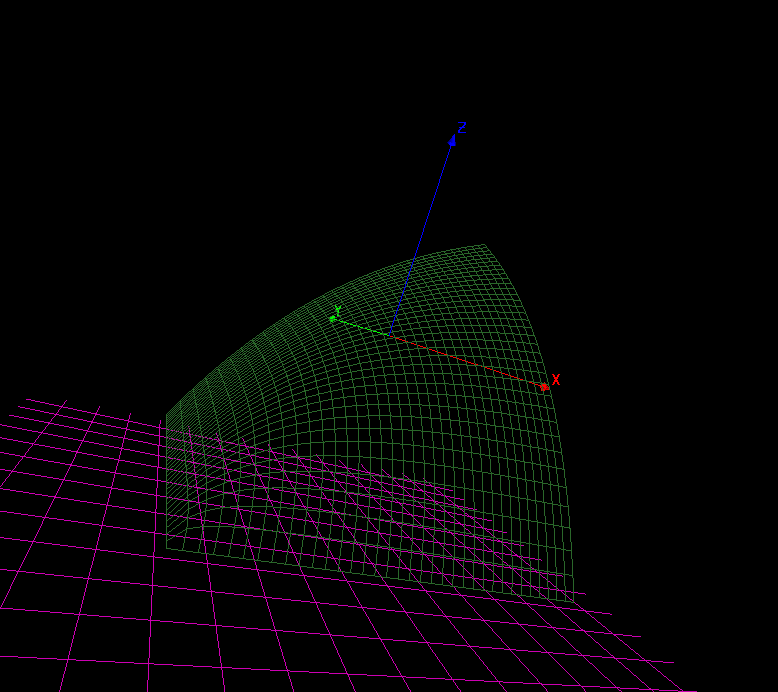
A priori, le problème n’est pas simple à résoudre, car la puissance et le NP résultent de calculs complexes – ils sont le résultat d’un calcul, et non les paramètres d’entrée, comme la vitesse! On peut visualiser ça en imaginant un plan dans lequel on fait varier V1 sur l’axe des X, et V2 sur l’axe des Y. A chaque point de coordonnées ( V1, V2), on fait correspondre sur l’axe Z la vitesse moyenne V = 2.V1.V2/(V1+V2). On obtient ainsi une surface S.
Trouver la répartition de vitesse (V1, V2) optimale revient à chercher sur cette surface le point le plus haut, tout en restant sur la ligne vérifiant la contrainte NP = constante (ligne de l’intersection de S avec la surface vérifiant NP = constante).
Heureusement, Excel vient nous aider à résoudre ça, grâce à la puissante fonction Solver. Solver utilise la méthode Generalized Reduced Gradient (GRG2) – nonlinear optimization code, qui a été développée par Leon Lasdon (University of Texas, Austin), et Alan Waren (Cleveland State University) – autrement dit, ça a l’air sérieux!
En fait il suffit de donner à Solver les cellules à faire varier (en l’occurrence V1 et V2), la cellule à maximiser (ici, la vitesse moyenne), et les contraintes à respecter (ici: NP = constante, par exemple 200W), et il déterminera les vitesses optimales V1 et V2 (et donc les puissances résultantes P1 et P2) pour maximiser la vitesse moyenne V.
J’ai rentré tout ça dans un tableur Excel, et il en ressort que oui, il faut appuyer plus fort quand on est face au vent – mais pas tant que ça.
Par exemple, un athlète ayant un NP de 200W et qui doit affronter un vent de face de 20 km/h a intérêt pour maximiser sa vitesse moyenne à produire 208,5W contre le vent (ce qui donne une vitesse de 20,9 km/h – planté face à un vent apparent de 40,9 km/h), et 178,5 W vent dans le dos (ce qui donne une vitesse de 42,4 km/h – vent apparent de 22,4 km/h).
Tant qu’à faire, j’ai aussi calculé ce que ça donnait pour une bosse, sans vent.
Un athlète ayant un NP de 200W et qui doit affronter une pente de 2,5% a intérêt pour maximiser sa vitesse moyenne à produire 215,9 W en montée (soit 22,4 km/h), et 156 W en descente (soit 39,5 km/h).
Ce que montre aussi ce calcul, c’est qu’il faut forcer face au vent, mais moins qu’en montée, car c’est moins rentable. Dans cet exemple, on ralentit plus face au vent que dans la bosse, et pourtant on a intérêt à mettre moins de puissance face au vent que dans la bosse. Ne pas trop regarder son compteur de vitesse mais écouter ses sensations (ou son capteur de puissance pour ceux qui en ont un).
J’ai mis la feuille Excel avec les calculs ici.
Optimiser sa puissance face au vent et aux bosses
Voilà, maintenant qu’on sait ce qu’il faut faire, il n’y a plus qu’à rouler.
Attention: un bug dans tout ça n’est jamais à exclure, donc si qqu’un se sent de relire et contrôler, welcome!

Très bon sujet !
Je te livre mon expérience sur l’im de Barcelone ou le vent omniprésent et fort à joue bien des tours au concurrents…
J’étais équipe d’une 808 avec un PowerTap et donc j’ai décide de me concentre sur les watt et pas sur la vitesse ( 4:58 au final et plutôt très bien au démarrage du marathon).
Sur la première boucle vent de face je n’ai pas arrête de me faire double, même si je doublais quelques concurrent parti avant moi en NAT.cest même devenu flippant jusqu’au retour ou la je les redoublais petit à petit vent dans le dos et les jambes autour du cou tellement il me fallait les tourner pour être à watt constant ( un peu plus de 220)
Sur la deuxième, je me fais encore doubler en revanche j’en double davantage vent dans le dos
Sur la troisième je ne me fais plus doubler voir j’en double vent de face et je vais continuer à doubler en ramassant quelques concurrent au passage qui n’hésiterons pas à drafter.
Je pose le bike comme jamais je ne l’ai posė, jambe nickel. La seul difficulté s’est de pédaler tout le temps de rester en prise pendant 5 heures, mais si entraîné, ca passe.
Cette position aéro est difficile à tenir sans se redresser tout le temps…. J’ai tenu sans grosses difficultés apparentes…. En revanche je l’ai payé à pieds… Diaphragme verrouillé…
En bref, je pense que la stratégie était la bonne…. En revanche il faut se relâcher de temps en temps si on veut courir….
j’ai eu une longue discussion avec un centralien au sujet du vent de face :
Est ce que c’est plus difficile pour qlq qui roule à 40kmh que pour qlq qui roule à 20kmh pour un même pourcentage de FCM ?
La fatigue est à peu près corrélée à la durée et au profil de FC de l’effort. Donc, quelle que soit la vitesse à laquelle on roule, si on roule à X% de FCM pendant une durée Y donnée, la fatigue ressentie devrait être la même. Maintenant, selon l’état de forme, l’entraînement et la capacité de l’athlète, l’un fera du 40km/h à 90% de FCM, et l’autre fera du 20km/h, sur le même trajet. En général, on considère qu’un athlète entraîné peut plus facilement tenir un pourcentage élevé de sa FCM – donc celui qui roule à 40km/h devrait moins se fatiguer que celui qui roule à 20 si tous les 2 sont à 90% de FCM sur le même trajet, pendant la même durée. On considère aussi qu’un cycliste bien entraîné aura une FCM en vélo plus proche de sa FCM réelle qu’un athlète non entraîné, qui aura typiquement une FCM vélo 5 ou 10 pulsations moins élevées que sa FCM course à pied. Une autre raison pour laquelle le cycliste entraîné souffrira moins en roulant à 40km/h à 90% de sa FCM réelle, que le débutant qui roule à 20 km/h à 90% de sa FCM, mais en étant probablement proche de 95% de sa FCM vélo.
he ben…
Bel effort !
Si et seulement si votre raisonnement dans ses détails est vérifié, le bon sens en action (subjectivement) n’est pas si loin de la loi du nombre.
Silb, vous êtes « le Reinhart & Rogoff » !
Encore bravo, et à nous lecteurs de relancer la mécanique et de plancher pour valider votre chose.
Je vais regarder ça.
Vectoriellement !
Juste comme ça, hors verif de l’excel (hein Silb, le Reinhart & Rogoff du triathlon) n’y aurait-il pas un bug sur la P_Air dans l’optique d’un aller-retour, vent de face = vent de dos ? « S », surface frontale, l’aéro c’est important, ça me chiffonne cette histoire.
Sans parler de Coggan.
NB : la NP me fait pédaler dans la semoule.
Sympa votre contre-devinette; j’ai comme une envie de couscous.
Bonjour Olivier,
Quelque chose me chiffonne dans P air.
La force de résistance est bien de type :
R_Air = 1/2 . ro . S . Cx . (V-Vent)^2
Mais pour la puissance nécessaire pour combattre cette force de résistance, n’est ce pas plutôt la vitesse de déplacement du cycliste qui intervient, et non sa vitesse relative au vent, de sorte que l’on aurait :
P_Air = V. R_Air
P_Air = 1/2 . ro . S . Cx . V . (V-Vent)^2
Bien vu!
C’est aussi par crainte de ce genre de bêtise que j’avais demandé à la fin de contrôler.
Je corrige…
Silb,
Je ne comprends pas votre non-prise en compte de l’aller et du retour.
Le cycliste a une tête de cul ?
« Quelle est l’allocation optimale de puissance entre l’aller et le retour qui maximise la vitesse moyenne tout en maintenant une NP constante? »
NP Normalized Poweraid toujours pas compris ??????
Poétiquement
Bonjour Olivier,
Petite contribution » calculer son SCx pour les pauvres » :
En descendant une bosse longue, bien régulière et rectiligne hier, sans pédaler ni freiner, ma vitesse a augmenté dans la pente, jusqu’à se stabiliser à une certaine valeur ( 55 km/h = assez précise ) pour une valeur de prente approximative de 6% ( pas très précis, mais « à l’oeil » ça correspondait assez bien avec ce qu’indiquait mon GPS ).
A cette vitesse stabilisée les données sont simples : la puissance générée par la descente est intégralement consommée par les frottement mécaniques et aérodynamiques.
On peut donc évaluer grossièrement son SCx, puisque comme P pente = P Air + P frottements, on a directement
SCx = 2.m.g. (p+K) / ro. V^2
Avec p=0.06 K=0.01 m=90 kg [ hum hum 🙁 ] V= 15.28 m/s ro = 1.205
SCx = 0.44, soit celle d’un amateur un peu dodu … caractéristiques que j’aurais bien du mal à contester.
Evidemment, c’est du grossier, puisque l’évaluation de la pente est approximative ( ainsi que l’absence de vent, que j’ai considéré nul par défait ), mais c’est quand même numériquement « dans les clous ».
Bonjour Silb,
Rien à voir directement avec le sujet de votre article, mais il me plait de vous conseiller la lecture d’un livre qui pourrait vous divertir en vous espaçant provisoirement de la gravité du monde.
Il s’agit de « La Théorie du Chaos » de Leonard Rosen au Cherche Midi (pour la traduction française).
http://la-vie-en-noir.blog.lejdd.fr/2013/08/18/la-theorie-du-chaos/
Une lectrice admirative de vos commentaires
Bonjour Silb,
Rien à voir directement avec le sujet de votre article, mais il me plait de vous conseiller la vision d’un film qui pourrait vous divertir en vous espaçant provisoirement de la gravité du monde.
Il s’agit de « Comment j’ai détesté les maths » d’Olivier Peyon.
http://www.lemonde.fr/culture/article/2013/11/26/comment-j-ai-deteste-les-maths-au-pays-merveilleux-des-mathematiques_3520193_3246.html
Tiens, n’y aura-t-il pas comme une espèce de déjà-lu ?
Une fidèle lectrice de votre blog qui vous souhaite bonne sérendipité dans votre quotidien !
I love your wp format, where did you get a hold of it?