Je ne suis guère accro aux jeux vidéos, mais j’avoue avoir craqué pour 2048, le jeu qui fait fureur en ce moment.
Il a un petit côté mathématique qui m’a attiré, et les puissances de 2 exercent toujours un certain magnétisme pour les informaticiens.
Je me suis posé la question de la stratégie, et j’ai trouvé un truc qui marche pas mal…
Le seul moyen de faire 2048, c’est de mettre ensemble deux 1024. Donc il faut d’abord faire un 1024. Mais pour faire un 1024, il faut faire deux 512. Donc on va devoir commencer par faire un 512, etc etc…
A la fin, on se rend compte que pour faire un 2048, il faut réaliser une chaîne: un 2 que l’on va transformer avec un autre 2 en 4, qui avec un autre 4 va faire un 8, qui avec un autre 8 va faire un 16 etc. jusqu’à 2048.
L’idée est donc de constituer une chaîne de cases adjacentes portant les puissances de 2 successives, et qui par effet de cascade vont permettre de passer à la puissance supérieure: supposons que j’ai une suite de cases adjacentes 2, 4, 8, 16 …. 2^n, alors, il suffit de joindre un 2 au premier 2 de la chaîne pour par effet de cascade générer un 2^(n+1): le 2 avec le 2 va faire un 4, qui avec le 4 va faire un 8, qui avec le 8 va faire un 16… qui avec le 2^n va faire un 2^(n+1).
L’objectif est donc de constituer une telle chaîne.
Pour cela, on applique un algorithme récursif.
Soit Cmax la case portant la valeur maximale de mon jeu, et 2^nmax la valeur de cette case.
Posons C = Cmax, et n = nmax.
1) L’objectif est de créer une case de valeur 2^(n-1) à côté de la case C.
2) Soit une telle case existe déjà, soit elle n’existe pas.
- Si elle existe déjà, on va alors l’appeler C, on donne à n la valeur n-1 (C porte alors la valeur 2^n), et on recommence en 1).
- Si elle n’existe pas, on garde la même case C inchangée, on donne à n la valeur n-1 et on recommence en 1).
Simple, non?
L’application d’un tel algorithme conduit à la fabrication d’une chaîne 2, 4, 8… 2^nmax qui par effet de cascade permettra ensuite simplement de créer une case 2^(nmax+1).
Un point clé est évidemment de conserver l’intégrité de la chaîne au cours des mouvements.
Pour cela, le mieux est d’avoir une chaîne qui serpente sur le jeu.
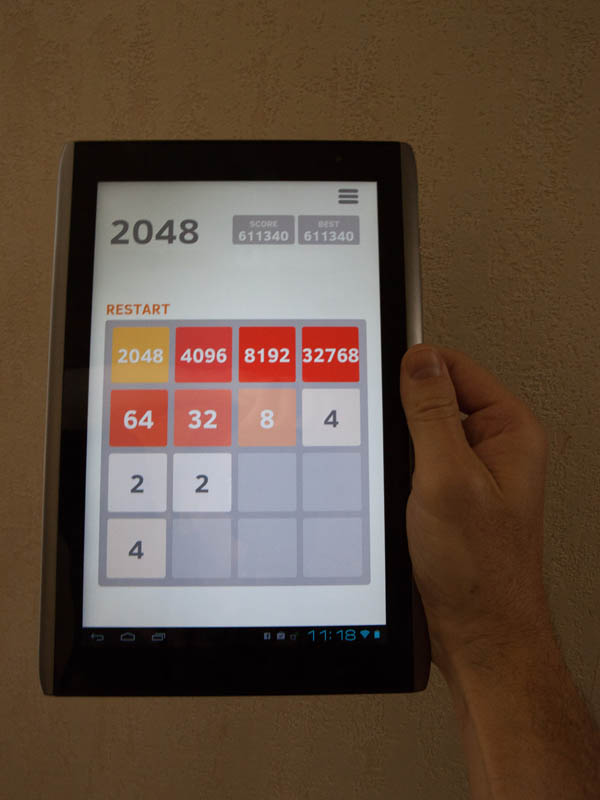
Par exemple, on décide de mettre la case max en haut à droite, et on fabrique ensuite le serpent avec les valeurs décroissantes des puissances de 2.
Évidemment, tout l’art consiste à éviter de se mettre dans une situation dans laquelle on ne pourrait pas exécuter la stratégie, en faisant un coup qui nous mettrait dans la suite dans l’obligation de faire un mouvement vers le bas. On essaye donc de garder les lignes du bas non vide et non pleines. Dans certaines situations, une approche probabiliste est nécessaire pour minimiser le hasard: on sait qu’un 4 a une chance sur 10 d’apparaître, et on peut évaluer la probabilité d’apparition sur une case donnée en fonction du nombre de cases libres.
Moyennant l’application de cette stratégie (et un peu de chance), on peut aller beaucoup plus loin que 2048, la limite étant alors surtout due au temps que votre boulot ou votre famille acceptera que vous y passiez! En tête de cet article, un exemple de partie en cours illustrant ces principes (qui m’a valu bien des remontrances de mes proches vu le temps passé…).
Sachant que l’on ajoute un deux dans 90% des cas et un 4 dans 10%, chaque coup fait en moyenne gagner 2,2. Pour arriver à 32768, il faut donc en moyenne 14895 coups. Si on compte une moyenne de 2 secondes par coup, ça fait 29790 secondes, soit plus de 8h de jeu en continu!
Pourquoi la revanche du serpent à plume?
On appellera Serpent à plume cet animal mythique et tout puissant, qui permettra un jour à son découvreur d’accéder au Graal: 2^16 = 65536.
Un jour peut-j’y arriverai! Peut-être en poussant jusqu’au bout la partie figurant en tête de cet article… Il faudra quand même 16h de jeu à 2 secondes par coup.
Une représentation du Serpent à Plume, à 15 coups de 65536.
| 4096 | 8192 | 16384 | 32768 |
| 2048 | 1024 | 512 | 256 |
| 16 | 32 | 64 | 128 |
| 8 | 4 | 2 | 2 |
Une fois le serpent à plume réalisé, on pourra s’attaquer à la réalisation du super-serpent à plume, qui mène à la valeur de case maximale possible sur 2048, 131072, mais là il faut encore plus de chance, car il faut que le dernier coup avant la complétion du super-serpent fasse apparaître un 4, et non un 2, ce qui n’a que 10% de chances de se produire. Autant dire il faudra faire en moyenne 10 serpents à plume avant de pouvoir réaliser un super-serpent (en supposant que tout se passe bien pour faire le super-serpent jusqu’à l’avant-dernier coup). Pas sûr qu’une vie y suffise!


Ça te bouffe tellement de temps que ça te laisse même pas 2 secondes pour corriger les fautes de frappe dans le titre !
Non, sans blague, retourne aux Sudokus…
Corrigé. Merci!
Bonjour Silb,
2048-2 = 2046
C’est un joli film. S’il vous reste encore du temps à perdre, vous pourrez le visionner.
Bon mardi.
« la courbure de l’espace-temps = superbe spectacle de l’amour »
Anagramme by Etienne Klein & Jacques Perry-Salkow.
Joli, non ? Encore ?
==> http://www.amazon.fr/Anagrammes-renversantes-sens-cach%C3%A9-monde/dp/2081272210
Ou passer commande à votre libraire-conseil.